This is not a complex task. With some simple mathematical calculation we can achieve this. A unit Quaternion can represent any arbitary a 3D orientation. Quaternions are nothing but 4Diamensional complex number. Visualizing quaternion is difficult when compared to affine matrices.
Rotation Using Quaternion
When user clicks on the scene we will get the points in window coordinates. we need to convert it into the correct world coordinates. If you are familar with opengl you can use gluUnProject API for this. Otherwise you can simply mul
tiply with corresponding matrices to get this.
So When user dragging the mouse we will get two points in world space ( since dragging is not a continus operation on computer unlike the physical draging process). We can generate a axis from this two points ( vectors ) by taking the cross product between them. The angle of rotation is nothing but arc cosine of dot prodcut of first and second vector.
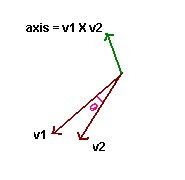
Now we can create a quaternion which represents the rotation around that axis.
Following code ilustrates this process. I used my Quaternion & vector classes to simplify the process.
Math3D::vector vtFrom;
Math3D::vector vtTo;
gluUnProject(m_PrePoint.x,m_PrePoint.y,0,fModeView,fProjection,iViewPort,&vtFrom.x,&vtFrom.y,&vtFrom.z);
gluUnProject(point.x,point.y,0,fModeView,fProjection,iViewPort,&vtTo.x,&vtTo.y,&vtTo.z);
vtFrom.y = -vtFrom.y;
vtTo.y = -vtTo.y;
vtFrom.normalize();
vtTo.normalize();
Math3D::vector vAxis = vtFrom.Cross( vtTo );
vAxis.normalize();
float fTheta = acos(vtFrom.Dot(vtTo));
Math3D::Quaternion qTmp;
qTmp.FromAxisAngle( vAxis, fTheta *2 );
qTmp.Normalize();
// multiply the current quaternion with the new one.
m_Quat *= qTmp;
m_PrePoint = point;
// normalise it.
m_Quat.Normalize();
Now the scene can be rotated with quaternion m_Quat and the scene will be rotated according the mouse movement made by the user.
6 comments:
Nice post. I have a question:
what if the magnitude of vtTo is so small that when you try to normalize you get a division by zero? (vtTo.normalize())
i don't think so.. because vtTo is the ray to screen.. it should be ok if u have correct projection matrix.
I am doing research for my university paper, thanks for your brilliant points, now I am acting on a sudden impulse.
- Laura
@Laura: Thanks for the appreciation.What is your topic ?
I think you may want to place a twitter icon to your site. I just bookmarked the url, although I must do it manually. Simply my advice.
Just a note on exceptional cases.
If v1 and v2 are parallel, you have axis = (0,0,0) and angle = 0.
You must make sure that your Quaternion class handles this; it can just ignore the 0 vector and return an identity quaternion [1 0 0 0].
If you just assign the quaternion components this way:
q[0] = cos(angle/2);
q[1:3] = axis.normalize() * sin(angle/2);
you will end up with the null quaternion [0 0 0 0], which will nullify any vector you multiply by it (the null quaternion hasn't unit magnitude, so you can't use it for rotations).
Another case is when v1 and v2 are antiparallel: you have axis = (0,0,0) and angle = pi.
You must handle this case, by selecting one of the infinite number of axes that are perpendicular to v1 (and to v2, of course). You must handle this explicitly, since the Quaternion class would have no way to know which axis is correct.
You can do it this way:
if(fabs(from.dot(vector(1,0,0))) < 0.707){
//not close to x axis, it will do
axis = from.cross(vector(1,0,0)).normalize();
}else{
//too close to x axis, use another one
axis = from.cross(vector(0,1,0)).normalize();
}
The angle, instead, is always correct as it is calculated now, by angle=acos(from.dot(to)), and it is always in [0,pi].
Post a Comment