Tracking results using meanshift and bhattacharya distance minimization technique.

In my last post I had said about mean shift algorithm . I  implemented tacking in video frames usiung meanshift algorithm and bhattacharya distance minimaization techniques( ask me if you need more details) . See the video below. ( Video resolution is poor.Please bear with me ).

In my opinion meanshift tracking is not so good,But still it can be useful on some occasions , where you don't want to know the shape of tracking object. It doesn't know anything about the shape of the object.There are other methods exists which are working in shape space and uses the edge detection for shape trasnformation. I have implemented one part of it, need to study some probabilistic modeling for completeing it.

Gradient vector calculation for non parametric data

Gradient vector points to the nearst position where a high rate of change can b e seen.

 Normally for a function it is obtained by applying the partial detivative operator. For example if we could represent the temperature inside a room by a function ( with parameter hight or time any conceiveing things )  , we could find the the gradient vector by applying partial derivative operator on that function. Using this technique we can go to the position where the temperature is highest than the current position.  We just need to simply go along the direction of gradient vector.

Okay .. Things are simple when we can paramterize things. Practically parametrization of physical things is not easy. In such situation we can find the gradient density vector using kernal density gradiant estimator.  In the follwing figure illustrates this mathematic technique. You can see that the circle is moved from it orginal position to the densest region (where more points present) .  I calculated gradient vector and moved the circle through that direction , thus finally the circle reached at the densest region . 

Used Epanechnikov Kernel for density estimation.

Arc ball rotation using Quaternion

Some times we need to rotate the scene for a better view. Rather than providing separate slider ball control or similar mechanisam to rotate around X,Y,Z axis it is better to do rotation with mouse and it will give a intutive feel to user. 

This is not a complex task. With some simple mathematical calculation we can achieve this. A unit Quaternion can represent any arbitary a 3D orientation. Quaternions are nothing but 4Diamensional complex number. Visualizing quaternion is difficult when compared to affine matrices.

Rotation Using Quaternion

When user clicks on the scene we will get the points in window coordinates. we need to convert it into the correct world coordinates. If you are familar with opengl you can use gluUnProject API for this.  Otherwise you can simply mul

tiply with corresponding matrices to get this.

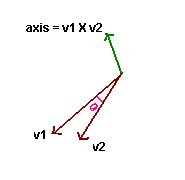
So When user dragging the mouse  we will get  two points in world space ( since dragging is not a continus operation on computer unlike the physical draging process). We can generate a axis from this two points ( vectors ) by taking the cross product between them. The angle of rotation is nothing but arc cosine of dot prodcut of first and second vector.

Now we can create a quaternion which represents the rotation around that axis.

Following code ilustrates this process. I used my Quaternion & vector classes to simplify the process.

Math3D::vector vtFrom;

Math3D::vector vtTo;

gluUnProject(m_PrePoint.x,m_PrePoint.y,0,fModeView,fProjection,iViewPort,&vtFrom.x,&vtFrom.y,&vtFrom.z);

gluUnProject(point.x,point.y,0,fModeView,fProjection,iViewPort,&vtTo.x,&vtTo.y,&vtTo.z);

vtFrom.y = -vtFrom.y;

vtTo.y = -vtTo.y;

vtFrom.normalize(); 

vtTo.normalize();

Math3D::vector vAxis = vtFrom.Cross(  vtTo );

vAxis.normalize(); 

float fTheta  = acos(vtFrom.Dot(vtTo));

Math3D::Quaternion qTmp;

qTmp.FromAxisAngle( vAxis, fTheta *2 );

qTmp.Normalize();

// multiply the current quaternion with the new one.

m_Quat *= qTmp;

m_PrePoint = point;

// normalise it.

m_Quat.Normalize();

Now the scene can be rotated with quaternion  m_Quat and the scene will be rotated according the mouse movement made by the user.

 

Pseudo Inverse calculation

Pseudo inverse matrix helps to get a satisfactory solution to linear equation which don't have any exact solution. This technique is used for curve fitting .

The pseudo inverse can be calculated like this . If A is the matrix

The pseudo inverse is this : Inverse[Transpose[a] * A ] * Transpose[A]

Normal inverse exists only for square matrix. So we can call this pseudo inverse as a general matrix inverse method.

Consider the following linear equations

5X1 + 4 X2 = 9

3X1 + 2X2 = 5

X1 + x2 = 3

Actually this set of equations doesn't have any exact solution.

A X R

5 4 x1 9

3 2 * x2 = 5

1 1 3

Clearly we can't calculate the normal inverse of A because it is not square matrix.

The pseudoinverse of A is

-.5 1.5 -1.0

.833 -1.833 1.333

So [Pseudoinverse]* [R] give the values for X1 and X2, which is the nearst solution for the equations.