Friday, December 4, 2009
Tracking using Active shape models
Friday, October 9, 2009
Ray - Circle intersection test.
If you are writing a game or any computer graphics applications you may want to check for intersections like triangle-triangle, triangle-ray, sphere-ray-sphere-sphere,Box-Triangle etc...There exists different algorithms for finding this.. Separating Axis theorem (SAT) seems to be a good option.
Following code written in c++ find intersection between a circle and line ( or ray-circle ). it will return true if there is intersection.Other function parameters are described in next lines.
vOrginCircle : center of the circle , r is the radius , vtLineStart: Line start point, vtLineEnd : Line end point, outIp : intersecting point..
As you can see it is easy to extend this method for finding ray-sphere intersection. just add a 'z' coordinate :)
bool IntersectLineCircle(vector vOrginCircle, double r,vector vtLineStart, vector vtLineEnd, vector& outIp)
{
vector vOrginNew = vOrginCircle - vtLineStart;
vector vtRay = (vtLineEnd - vtLineStart).normalize();
double b = vOrginNew.x* vtRay.x + vtRay.y * vOrginNew.y;
double c = r*r - ( vOrginNew.Norm2() );
double a = vtRay.Norm2(); // Norm2() is x*x + y*y
double diva = 1.0F/a;
// Negative doesn't have square root.
if( (b*b + a * c ) <= 0 ) return false;
double b4ac = sqrt( (b*b + a * c ) );
double l1 = (b - b4ac) * diva;
double l2 = (b + b4ac) * diva;
// we need the closest intersection point.. so find smaller l.
// To get the other end , just change the comparison operator.
double l = l1 <>
// find the intersecting point
outIp = (vtRay * l) + vtLineStart;
return true;
}
Friday, May 8, 2009
Friday, April 24, 2009
2X2 Matrix inversion.
Sometimes it is needed to find the inverse of a simple 2x2 matrix. For this there is a simple method exitst , we don't have to apply any gauss jordan method or crammers etc.
The Matrix A = [ a00 a01 ]
[ a10 a11 ]
then the inverse is 1 [ a11 -a01 ]
--- x [ ]
| A | [ -a10 a00 ]
| A | is determinent of matrix A which is a00 * a11 - a10 * a01
Monday, April 20, 2009
State estimation using Kalman filter
Kalman filter helps to find the correct state of a linear system , provided the approximate state of the system at time 't'. It has wide application in the following fields Aerospace,computer vision, signal processing etc.
Let 'St' be the state variable at time t
St1 = A * St0 + V ,
V is the random noise with mean = 0
A is the gain Matrix of the system.
Let Mt be the measurment variable. Measurment is the approxiamte state at time t. Kalman filter can predict the correct state from this measurment( also depending on other params etc ).
Mt1 = H * St1 + W
H is the gain Matrix.
W is the random noise with mean = 0.
The interseting thing is usually Mt1 is known at time t1 and we want to find the st1 which is the correcte state at time t1 from this Mt1.
Kalman filter uses kalman gain to compute the state St.
St = St + Kt*( Mt - H*St ) , Kt is the gain matrix. and the new St is calculatd using the kalman gain Kt.
The noise is represented in this system using a covariace matrix. Let P represent the noise of function V ( system noise ) and R represent the noise during measurment.
I am omitting the detailed derivation of equations here. The final equation and steps are shown below.
At time 't' do the follwing to estimate the correct state St.
Update the state vector and measurment covariance matrix.
St = A * St
P = A * P * Transpose[P]
find the kalman gain for this.
K = A*P0*Transpose[H]* Inverse[ ( H*P0*Transpose[H] + R) ]
Mt = Do measurment here and assign to Mt.
Calcualte the estimated state St.
St = St + K* ( Mt - H*St );
Finally update the state updation covariance matrix P
P = P - K*(H*P )
Repeat these steps for each measurment.Following figure shows the result.
The measurment data 'Mt' , which is affected by noise.and rectified data St which is the output of Kalman filter and it gives us better prediction of the state.


Sunday, March 29, 2009
Tracking results using meanshift and bhattacharya distance minimization technique.
In my last post I had said about mean shift algorithm . I implemented tacking in video frames usiung meanshift algorithm and bhattacharya distance minimaization techniques( ask me if you need more details) . See the video below. ( Video resolution is poor.Please bear with me ).
In my opinion meanshift tracking is not so good,But still it can be useful on some occasions , where you don't want to know the shape of tracking object. It doesn't know anything about the shape of the object.There are other methods exists which are working in shape space and uses the edge detection for shape trasnformation. I have implemented one part of it, need to study some probabilistic modeling for completeing it.
Thursday, March 19, 2009
Gradient vector calculation for non parametric data
Normally for a function it is obtained by applying the partial detivative operator. For example if we could represent the temperature inside a room by a function ( with parameter hight or time any conceiveing things ) , we could find the the gradient vector by applying partial derivative operator on that function. Using this technique we can go to the position where the temperature is highest than the current position. We just need to simply go along the direction of gradient vector.
Okay .. Things are simple when we can paramterize things. Practically parametrization of physical things is not easy. In such situation we can find the gradient density vector using kernal density gradiant estimator. In the follwing figure illustrates this mathematic technique. You can see that the circle is moved from it orginal position to the densest region (where more points present) . I calculated gradient vector and moved the circle through that direction , thus finally the circle reached at the densest region .
Used Epanechnikov Kernel for density estimation.

Wednesday, March 4, 2009
Arc ball rotation using Quaternion
This is not a complex task. With some simple mathematical calculation we can achieve this. A unit Quaternion can represent any arbitary a 3D orientation. Quaternions are nothing but 4Diamensional complex number. Visualizing quaternion is difficult when compared to affine matrices.
Rotation Using Quaternion
When user clicks on the scene we will get the points in window coordinates. we need to convert it into the correct world coordinates. If you are familar with opengl you can use gluUnProject API for this. Otherwise you can simply mul
tiply with corresponding matrices to get this.
So When user dragging the mouse we will get two points in world space ( since dragging is not a continus operation on computer unlike the physical draging process). We can generate a axis from this two points ( vectors ) by taking the cross product between them. The angle of rotation is nothing but arc cosine of dot prodcut of first and second vector.
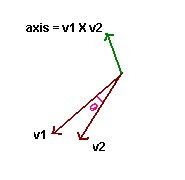
Now we can create a quaternion which represents the rotation around that axis.
Following code ilustrates this process. I used my Quaternion & vector classes to simplify the process.
Math3D::vector vtFrom;
Math3D::vector vtTo;
gluUnProject(m_PrePoint.x,m_PrePoint.y,0,fModeView,fProjection,iViewPort,&vtFrom.x,&vtFrom.y,&vtFrom.z);
gluUnProject(point.x,point.y,0,fModeView,fProjection,iViewPort,&vtTo.x,&vtTo.y,&vtTo.z);
vtFrom.y = -vtFrom.y;
vtTo.y = -vtTo.y;
vtFrom.normalize();
vtTo.normalize();
Math3D::vector vAxis = vtFrom.Cross( vtTo );
vAxis.normalize();
float fTheta = acos(vtFrom.Dot(vtTo));
Math3D::Quaternion qTmp;
qTmp.FromAxisAngle( vAxis, fTheta *2 );
qTmp.Normalize();
// multiply the current quaternion with the new one.
m_Quat *= qTmp;
m_PrePoint = point;
// normalise it.
m_Quat.Normalize();
Now the scene can be rotated with quaternion m_Quat and the scene will be rotated according the mouse movement made by the user.
Tuesday, March 3, 2009
Pseudo Inverse calculation
The pseudo inverse can be calculated like this . If A is the matrix
The pseudo inverse is this : Inverse[Transpose[a] * A ] * Transpose[A]
Normal inverse exists only for square matrix. So we can call this pseudo inverse as a general matrix inverse method.
Consider the following linear equations
5X1 + 4 X2 = 9
3X1 + 2X2 = 5
X1 + x2 = 3
Actually this set of equations doesn't have any exact solution.
A X R
5 4 x1 9
3 2 * x2 = 5
1 1 3
Clearly we can't calculate the normal inverse of A because it is not square matrix.
The pseudoinverse of A is
-.5 1.5 -1.0
.833 -1.833 1.333
So [Pseudoinverse]* [R] give the values for X1 and X2, which is the nearst solution for the equations.
Friday, January 23, 2009
Eigen Vector
Today i just created one application to demonstrate the use of eigen vectors.
It is only for 2 diamensional things. Beacuse in 3D calculating eigen vector is a complex process ( It depends), involving linear equation solving , and cubic equations' root finding.
You canse see the eigen axis can be used for finding the OBB( oriented bounding boxes) for a set of points. This has significance inmportant in Computer graphics.
One more interesting thing is eigen vector of a rotaion matrix is actually its axis of rotation (similar to curl of a vector field , but curl calculation is easier).
It is only for 2 diamensional things. Beacuse in 3D calculating eigen vector is a complex process ( It depends), involving linear equation solving , and cubic equations' root finding.
You canse see the eigen axis can be used for finding the OBB( oriented bounding boxes) for a set of points. This has significance inmportant in Computer graphics.
One more interesting thing is eigen vector of a rotaion matrix is actually its axis of rotation (similar to curl of a vector field , but curl calculation is easier).
Subscribe to:
Posts (Atom)

